| 3.4.1.1 Scalars and vectors |
Nature of scalars and vectors. |
Examples should include: velocity/speed, mass, force/weight, acceleration, displacement/distance. |
|
| |
The addition of vectors by calculation or scale drawing. |
Calculations will be limited
to two perpendicular vectors.
Scale drawings may involve vectors at angles other than 90°. |
Don't forget to use the interactive XL spreadsheet on vectors and projectiles |
| |
The resolution of vectors into two components at right angles to each other; |
Examples should include the components of forces along and perpendicular to an inclined plane. |
Note that the data sheet does NOT give you the basic trig info. You need to KNOW that!
Also you need to know Pythagoras' Theorem |
| |
Conditions for equilibrium for two or three coplanar forces acting at a point;
Appreciation of the meaning of equilibrium in the context of an object at rest or moving with constant velocity.
|
Problems may be solved either by using resolved forces or by using a closed
triangle. |
MS 0.6, 4.2, 4.4, 4.5 / PS 1.1 Investigation of the conditions for equilibrium for three coplanar forces acting at a point using a force board. |
| 3.4.1.2 Moments |
Moment of a force about a point defined as force × perpendicular distance from the point to the line of action of the force; |
'torque' as a term has now been removed from the syllabus - but it doesn't hurt you to know it.... |
moment = Fd
Don't forget the interactive XL spreadsheet on moments |
| |
Couple as a pair of equal and opposite forces
Moment of a couple defined as force × perpendicular
distance between the lines of action of the forces.
|
|
|
| |
The principle of moments and its applications in simple balanced situations. |
|
For equilibrium:
Σ clockwise moments = Σ anticlockwise moments |
| |
Centre of mass
Knowledge that the position of the centre of mass of uniform regular solid is at its centre. |
Calculations of the position of the centre of mass of a regular lamina are not expected. |
|
| 3.4.1.3 Motion along a straight line |
Displacement |
|
Displacement is distance moved in a particular direction. You must understand the difference between distance and displacement! |
| |
speed |
|
You met speed at KS3 |
| |
velocity |
MS 3.6, 3.7 / PS 1.1, 3.1 - Distinguish between instantaneous velocity and average velocity |
|
| |
and acceleration. |
|
|
| |
Representation by graphical methods of uniform and non-uniform acceleration;
|
MS 3.5, 3.6 Measurements and calculations from displacement–time, velocity–time and acceleration–time graphs. |
You need to know the dynamics graphs that you met at GCSE
You have to know how to draw graphs to a high standard - and how to find gradients and areas under graphs (differentiation and integration will not be called for) |
| |
Interpretation of velocity-time and displacement-time graphs for uniform and non-uniform acceleration; eg graphs for motion of bouncing ball. |
Need to understand the physical significance of areas under graph lines and gradients. |
Area under a v/t graph between two times is the distance travelled in that time interval
Gradient of s/t graph is velocity and gradient of a/t graph is acceleration |
| Equations for uniform acceleration |
|
|
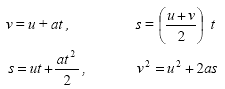
Don't forget the interactive XL Spreadsheets |
| |
Acceleration due to gravity, g;
|
Required practical 3: Determination of g by a freefall method.
MS 0.3, 1.2, 3.7 / AT d Students should be able to identify random and systematic errors in the experiment and suggest ways to remove them.
MS 3.9 Determine g from a graph |
| 3.4.1.4 Projectile motion |
Independent effect of motion in horizontal and vertical directions of a uniform gravitational field. |
Problems will be solvable using the equations of uniform acceleration. The memorising of projectile equations is not required. |
Don't forget the interactive XL Spreadsheets |
| |
Qualitative treatment of friction.
Qualitative treatment of lift and drag forces. |
Distinctions between static and dynamic friction will not be tested. |
PS 2.2, 3.1 Investigation of the factors that determine the motion of an object through a fluid. |
| |
Terminal speed
Knowledge that air resistance increases with speed. |
Qualitative understanding of the effect of air resistance on the trajectory of a projectile and on the factors that affect the maximum speed of a vehicle. |
|
| 3.4.1.5 Newton’s laws of motion |
Knowledge and application of the three laws of motion in appropriate situations.
|
|
You met these at GCSE
Make sure you can quote them!
But note that Ft = Δmv is on the A2 syllabus not the AS one!
as is conservation of momentum - so don't worry about it at AS! |
| |
For constant mass, F = ma |
Interactive XL Spreadsheet |
PS 4.1 / MS 0.5, 3.2 / AT a, b, d Students can verify Newton’s second law of motion.
MS 4.1, 4.2 Students can use free-body diagrams.
|
| 3.4.1.6 Momentum |
Momentum
Principle applied quantitatively to problems in one dimension. |
momentum = mass × velocity
p = mv |
MS 2.2, 2.3 Students can apply conservation of momentum and rate of change of momentum to a range of examples. |
| |
Force as the rate of change of momentum
F= ∆(mv)/ t∆ |
|
|
| |
Impulse = change in momentum
F∆t =∆(mv) |
where F is constant |
Recall the terms momentum and impulse and their units.
Interpret force v. time graphs - area under the graph is the impulse. |
| |
Significance of area under a force-time graph.
Principle of conservation of linear momentum applied to problems in one dimension.
Elastic and inelastic collisions; explosions.
|
Quantitative questions may be set on forces that vary with time.
Impact forces are related to contact times (eg kicking a football, crumple zones, packaging).
Appreciation of momentum conservation issues in the context of ethical transport design. |
Quote the principle of conservation of linear momentum.
Explain the difference between elastic and inelastic collisions.
 Momentum Structured questions Momentum Structured questions
 Momentum Multiple Choice Momentum Multiple Choice
|
| 3.4.1.7 Work, energy and power |
Energy transferred, W = Fs cos θ
rate of doing work = rate of energy transfer,
P = ∆ W /∆ t = Fv
efficiency = useful output power /input power
|
MS 0.3 / PS 3.3, 4.1 / AT a, b, f. Investigate the efficiency of an electric motor being used to raise a mass through a measured height.
Students should be able to identify random and systematic errors in the experiment and suggest ways to remove them |
 Significance of the area under a force–displacement graph. Significance of the area under a force–displacement graph.
Quantitative questions may be set on variable forces.
Efficiency can be expressed as a percentage. |
| 3.4.1.8 Conservation of energy |
Principle of conservation of energy, |
Applied to examples involving gravitational
potential energy, kinetic energy and work done against resistive forces - such as friction and air resistance. |
MS 0.4, 2.2 Estimate the energy that can be derived from food consumption.
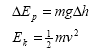
|


