Half Life and Rate of Decay

The half-life of a radioactive isotope is the time it takes for the number of nuclei of the isotope in a sample to halve.

Or you could define it as:

The time it takes for the count rate (or activity) of a sample containing the isotope to fall to half its initial level - after elimination of background rate.

Click here to go to a page describing a GCSE level practical to determine half life.

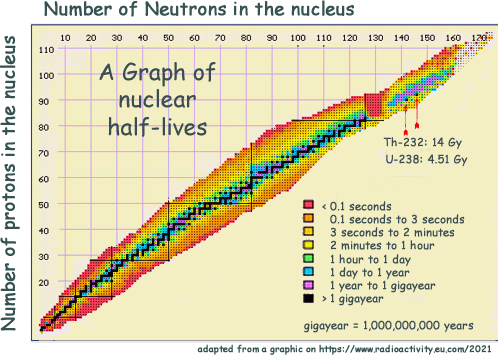
Range of half-lives

This map of nuclei shows the massive range of half-lives that isotopes have - from less than a second to billions of years.

The black central line plots nuclei that are either stable or have a half-live longer than a billion years. You can see that the further away anisotope is from that stable line the shorter the half life is. Those nuclei which only survive for a fraction of a second, (coloured in red) are found at the outermost edges of the plot. Those are mainly 'man made' - they would not exist for very long in nature for us to have discovered them!

A group of very heavy, very unstable nuclei can also be found around the 130 neutron, 85 proton mark. Among even heavier nuclei, we find an island of comparative stability (in mauve), where a group of isotopes have a half-life between the one- and the billion-year mark.

The two heaviest natural nuclei, thorium 232 and uranium 238, are the solitary black dots in the mauve island.

Hazard related to Half Life

You may think that those with very short half lives do not matter - but they do.

A sample containing a billion short living isotope nuclei will deliver a very intense burst of radiation instantly - whereas a similar sized sample of long half life nuclei would register very little activity... but would remain radioactive for a long time.

When performing tasks you need an isotope with a suitable half life.

GCSE standard questions on half life

At GCSE you do not have the maths skills to cope with the equations in the A Level section below. You just need to know that the half-life is the time taken for half on the sample you have to decay.

Working out a half-life for a GCSE standard question is best explained with an example:

Suppose you have a radioisotope producing a count rate of 640 Bq.

After 14 minutes the count rate had dropped to 5 Bq.

What would be the half-life?

Well, it would take:

one half-life for the activity to drop from 640 Bq to 320 Bq

a second half life for the activity to drop to 160Bq

a third for it to drop to 80Bq

a fourth for it to drop to 40 Bq

a fifth for it to drop to 20 Bq

a sixth for it to drop to 10 Bq

and a seventh for it to drop to 5 Bq

So it would take seven half lives for the activity to drop from 640 Bq to 5 Bq.

The time for this to happen was 14 minutes

14 ÷ 7 = 2

so the half-life must be 2 minutes.

Sometimes questions include a value for the background rate.

This is the rate of activity that is due to background radiation NOT the sample and must therefore be deducted before any calculations are done.

The background count for the laboratory was found to be 6 Bq.

It took 10 minutes for the count-rate to drop from 102 Bq to 12 Bq when a radioactive substance's count rate was being measured.

What was the half-life of the sample?

Initial count-rate due only to the sample was (102-6) Bq = 96 Bq

Final count-rate due only to the sample was (12-6) Bq = 6 Bq
 

It would take:

one half-life for the activity to drop from 96 Bq to 48 Bq

a second half life for the activity to drop to 24 Bq

a third for it to drop to 12 Bq

a fourth for it to drop to 6 Bq

 

So it would take four half lives for the activity of the sample alone to drop from 96 Bq to 6 Bq.

The time for this to happen was 10 minutes so the half-life must be 2.5 minutes.

 

'A Level' Half Life Calculations: Rate of Radioactive Decay

The rate of decay is the number of radioactive atoms that emit nuclear radiation in one second. This is effectively the same as the activity (A) of the sample.

It is the gradient of a graph of the number of radioactive nuclei (n) in a sample against time (t) - as the gradient is by nature negative and we want 'activity' to be positive:

^{- dn}/_dt = A

It is measured in becquerel (Bq).

It is sometimes referred to as the 'count' for a sample.

You should realise that the geiger counter only gives an indication of the activity as it does not detect ALL particles - only a proportion of them!

Changing the setting on the meter changes the 'count' but not the activity it is measuring. When doing an experiment it is important not to change the settings on your counter - keep them the same! You can then make valid comparisons.

The decay Constant (λ)

The rate of decay or activity (A) depends on the number of radioactive atoms present (n).

It is proportional to the number that have not yet decayed in the sample 'n'.

The constant of proportionality is called the decay constant and given the symbol λ (lamda).

A = λn

The decay constant is characteristic to each radioactive isotope.

It is the probability of a decay occurring.

We can calculate the expected activity of a sample if we know its size and decay constant.

If we integrate ^{- dn}/_dt = λ n with respect to t we get:

n = n₀e^-λt

Now as n = A/λ we can substitute and cancel to get:

A = A₀e^-λt

Half Life

The maths for this used to be expected - but no longer is in most syllabuses -

but it is 'good for your souls' to see where the equations on your equation sheet come from.

Half life is the time taken for half of the sample to 'decay'.

So let n₀ (the original number when t = 0s) = 1

then n (the number when t = T_½) = ½

Substituting those values into the equation above we get:

½ = e^-λT½

taking natural logs:

- ln 2 = - λT_½

so

ln 2 = λT_½

Rearranging we get that the half life of a radioactive isotope is inversley proportional to the decay constant.

T_½ = (ln 2)/λ

The activity of radioisotopes decreases exponentially with time

After a certain time period the amount of substance in your sample that has yet to decay has been halved.

This is the case no matter when you start to measure the activity of the sample. The time taken for this 'halving' of activity is called the half-life.

Half-lives vary widely from microseconds to millions of years!

Uranium-238 has a half-life of 4.5 x 10⁹ years (4,500,000,000 years) whereas Polonium-212 only has a half-life of 3 x 10^-7 seconds (0.000 000 3 seconds).

Also the tables of isotopes in the decay series section show a wide variation in half-lives.