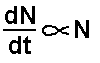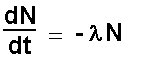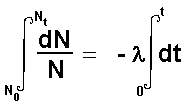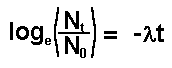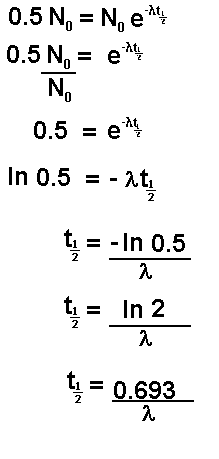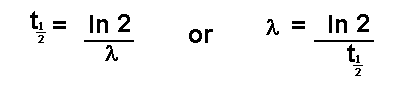Topic Menu

Cyber-chess a chess instruction site

Radioactive Decay at 16+

All radioactive decay occurs in such a way as the number of atoms 'decaying' in unit time (dN/dt) is directly proportional to the number of undecayed radioactive atoms present in the sample at that time (N).

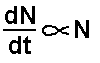
The mathematics of statistics applies (a very large number of 'events' needs to be considered). A constant of proportionality l (called the decay constant) replaces the proportionality symbol, thereby making the equation simpler:

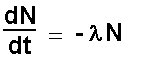
With time the number of undecayed atoms decreases. The activity decreases therefore the change in activity is negative. Adding the negative sign allows us to have a positive value for the activity. Note the negative sign!

The type of equation is called a differential equation. Calculus can be used to integrate this giving and expression that incorporates both the initial number of atoms present and the final number present after a time interval 't'

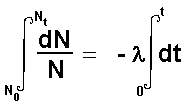
When solution of this equation is:

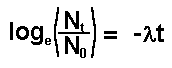
Therefore

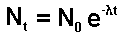
Thus we have a mathematical expression that shows that radioactive decay is exponential.



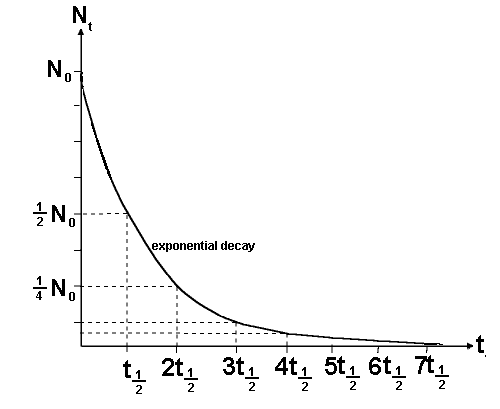
If Nt is half of N0 then the time t is the time taken for half of the sample to undergo spontaneous disintegration or decay. This is termed the half life and is given the symbol

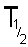  or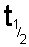 

Let us follow the mathematics of this through for a half life value:

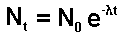
Now let us insert the number of atoms present in terms of the original number:

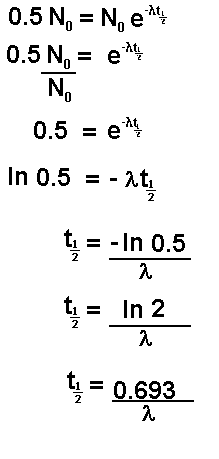
How this is achieved should be understood. If necessary look in the mathematics section at the background on use of logs.

It is important that l can be found directly from the half life and vice versa is remembered.

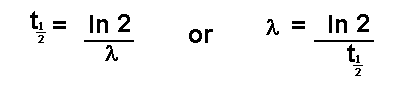
A similar calculation can be done to find the time taken for a certain percentage of a sample to decay.
 

Try the following question:
The half-life of cobalt 61 is 100 minutes. How long does it take for the activity of the sample to fall to 80% of its initial value?


or to find the percentage left after a certain time lapse
 

Try this question:
The half-life of radioactive zinc is 50 hours. Find the percentage loss of activity which occurs for a sample each hour.

 

Now use the interactive spreadsheets to investigate the half life idea in a little more depth...