Topic Menu

Cyber-chess a chess instruction site

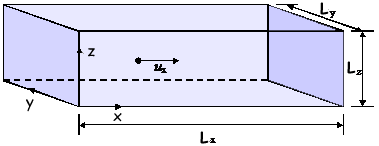
A level: Kinetic Theory Questions

Q1. A single gas molecule of mass m is moving in a rectangular box with a velocity of ux in the positive x-direction, as shown in the diagram. The molecule moves backwards and forwards in the box, striking the end faces normally and making elastic collisions.

(a)

(i) Show that the time, t, between collisions with the shaded face, is t = 2Lx/ux

(ii) In terms of m and ux write down an expression for the change of momentum per collision with the shaded face.

(2 marks)

(b) If it is assumed that the box contains N identical molecules, each of mass m, all moving parallel to the x-direction with speed ux and making elastic collisions at the ends, show that the average force, F, on the shaded face is given by F = Nmux2/Lx

(2 marks)

(c) In a better model of molecular motion in gases, molecules of mean square speed are assumed to move randomly in the box.

(i) By considering this random motion, obtain an expression for ux2in terms of .

(ii) Show that a better expression for F is F = Nm/(3Lx)

(iii) Hence derive the equation pV = 1/3 Nm

(5 marks)

(Total 9 marks)