Topic Menu

Cyber-chess a chess instruction site

Nuclear Radius

Q6. The high energy electron diffraction apparatus represented in the diagram below can be used to determine nuclear radii. The intensity of the electron beam received by the detector is measured at various diffraction angles, θ.

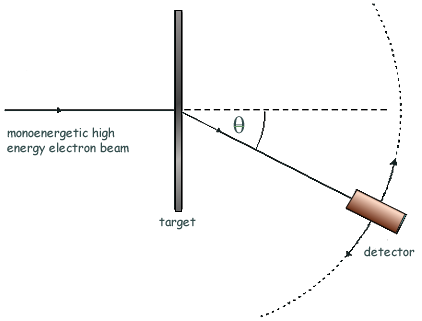
(a) Sketch on the axes below a graph of the results expected from such an electron diffraction experiment.

(2 marks)

(b)

(i) Use the data in the table below to plot a straight line graph that confirms the relationship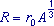

 

element

radius of nucleus

R /10–15m
nucleon number; A
lead
6.66
208
tin
5.49
120
iron
4.35
56
silicon
3.43
28
carbon
2.66
12

 

(ii) Estimate the value of r0 from the graph.

(5 marks)

(c) Discuss the merits of using high energy electrons to determine nuclear radii rather than using α particles.

(3 marks maximum)

(Total 10 marks)