The photoelectric effect
Work function Φ, threshold frequency fo, photoelectric equation hf = Φ + Ek; (the stopping potential experiment is not required) |

(QUESTIONS 1-4: L&R Ex 27.1) |
- Explain the underlying principles behind the photoelectric effect, including a derivation of Einstein’s equation in terms of energy conservation
- Understand the term photon and calculate the number of photons in a light beam
- Derive the equation: hf = Φ + Ek
- Explain that the work function is the energy with which each electron is bound to the surface of the metal (and therefore the energy that is required to release it from the metal)
|
Collisions of electrons with atoms: Ionisation, excitation
The electronvolt
Understanding of the role of ionisation and excitation in the fluorescent tube;
|
|
- Recall the structure of the atom to include the energy level model for electrons
- Recall the definition of the electronvolt |
| Energy levels and photon emission line spectra (e.g. of atomic hydrogen) as evidence of transitions between discrete energy levels
Energy levels, photon emission : hf = E1 - E2 |

Ciccotti and Kelly pp 72-79
L&R Ex136 Q1, 2, 5, 7
(QUESTION 7: L&R Ex 27.1)
Muncaster G19-G21 |
- There are two types of line spectra: absorption and emission
- Explain the difference between ionisation and excitation and apply this to the operation of a fluorescent tube
- Explain the origin of line spectra and use this as evidence to support the model of discrete energy levels
- Recall the equation hf = E1 - E2
|
Wave-particle duality
Candidates should know that electron diffraction suggests the wave nature of particles and the photoelectric effect suggests the particle nature of electromagnetic waves; (details of particular methods of showing particle diffraction are not expected)
de Broglie wavelength
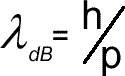
where mv is the momentum p
|

Ciccotti and Kelly pp 83
(QUESTIONS 5-6: L&R Ex 27.1)
|
- Recall the evidence for wave and particle behaviour in light and matter and indicate practical methods that can be used to demonstrate these properties
- Recall the equation for the de Broglie wavelength
- Recognise the effect of particle speed on wavelength and the potential diffraction effect that could be obtained
|


