Topic Menu

Cyber-chess a chess instruction site

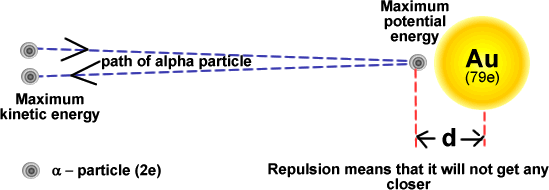
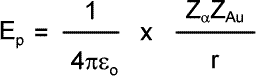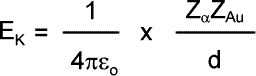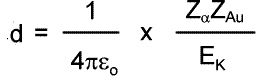Scattering - to probe the nucleus

The mathematics involved in Rutherford Scattering analysis is too high level for this standard of study. We can however apply some basic ideas from the level at which you are at to understand how alpha scattering can be used to determine the size of the nucleus.

Consider a head-on collision between an alpha particle and a gold nucleus.

Initially the alpha particle has only kinetic energy EK. As it approaches the gold nucleus it suffers repulsion by the 79 protons within that nucleus. Its kinetic energy changes into electric potential energy EP.

The potential energy of the alpha particle at its closest approach is:

All of this energy is equivalent to the kinetic energy of the alpha particle before its approach:

Therefore 'd' can be calculated.

Using the data in the diagram calculate the distance of closest approach for alpha particles of 5 MeV energy.

5 MeV = 5 x 106 x 1.6 x 10-19 J = 8.0 x 10-13 J

d = ((2 x 79) x (1.6 x 10-19)2 / (4 (8.85 x 10-12 x 8.0 x 10-13))

    = 4.5 x 10-14 m

The scattering of electrons from nuclei has given us the most precise information about nuclear size and charge distribution. The electron is a better nuclear probe than the alpha particles of Rutherford scattering because it is a point particle and can penetrate the nucleus but the mathematics and physics involved is to complicated for this level of study.