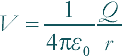Electric/Electrostatic Potential

Electric (or electrostatic) potential has the symbol: V

It can be defined as:

The work done in bringing unit positive charge from infinity to that point in the field.

OR

The potential energy per unit of charge associated with a static (time-invariant) electric field.

It is a scalar quantity

It is measured in volts (V) - which can be confusing an lead to you writing things like V = 4.56V - which is obviously wrong mathematically - so develop a style for writing the V for electric potential in a different way to the V you use for volts!

The equation:

V = electrostatic potential

Q = charge causing the electrostatic potential

r = distance from the charge to the point at which you are measuring the electrostatic potential.

Potential difference

The difference of electrical potential between two points is known as potential difference or voltage.

You are used to living in the matter dimension - one in which objects 'gravitate' towards or away from a point because of the gradient of the landscape around them because they possess mass.

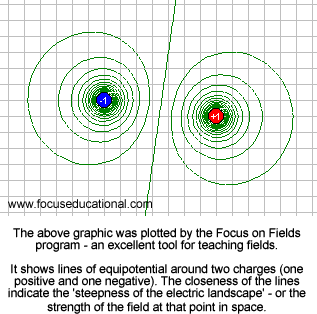
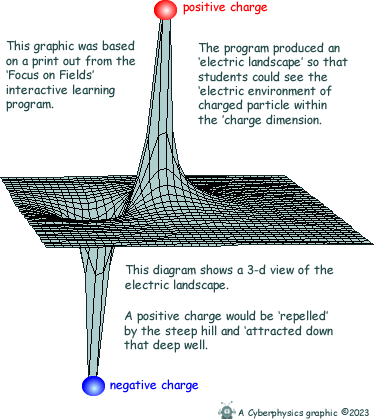
A stationary ball will always roll downhill if placed on a sloping surface - moving from a higher gravitational to lower gravitational state. It will remain stationary on a level surface - as thereis no route to a lower gravitational state.

Now imagine an 'electric dimension'. One where charges are much more important than mass. Charges create the landscape that all other charged objects react to.

Look at the above definition of electric potential and think of it in terms of graviational potential.

We could say that gravitational potential (position in the gravitational field) is the potential energy per unit of weight associated with a gravitational field - the two are comparable:

 

If you think of the electric field as a 'landscape for charge' - hills and vales that will make a free 'rolling' charge accelerate and/or decelerate as it makes its way through it, then you can think of electric potential as the 'height' of various points on that 'landscape'. When the 'potential difference' causes a slope charges will move along the electric potential gradient.

You can plot points of equipotential around a charge to get a 'contour map' of that electric landscape. A point in space an infinite distance from any charge is said to be at zero volts. On the 3-d diagram below you see that as a 'plane' - a flat area in the electric dimension landscape that goes off into infinity. Look at how the 3-d diagram shows a steeper gradient to the field between the charges - to correspond to the closer contour lines. The gradient of field is called the electric intensity or electric field strength.

Electric potential is a scalar value.

This concept gives people problems because Electric Potential has a sign (positive or negative).

You need to think of the sign as an indication of whether that point in space is above or below the zero plane.

To work out the potential of a point affected by the fields of several charges you need to work out what effect each charge has on the height of the 'terrain' at that point.

A positive charge will lift it above zero and a negative charge below zero.

You simply add the 'adjustments in electric height' together to get the final value.

Sample Question:

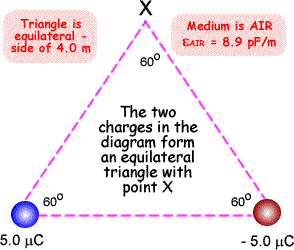
What is the electrostatic potential at point X?

Using the equation:

We first of all work out the potential at X from each of the charges.

V = Q/(4πε₀r)

The positive charge:

V = 5.0 x 10^-6/(4π x 8.9 x 10^-12 x 4.0)

V = 1.12 x 10⁴ V

The negative charge:

V = - 5.0 x 10^-6/(4π x 8.9 x 10^-12 x 4.0)

V = - 1.12 x 10⁴ V

We then add them:

V_x = 1.12 x 10⁴ - 1.12 x 10⁴

V_x = 0.0 V

The result from the positive charge is 1.12 x 10⁴ volts - this means that point X is 'lifted' by the presence of that charge and from the negative charge it is -1.12 x 10⁴ volts - meaning that point X is lowered by the presence of that charge.

The sum of these is zero volt potential (X is at zero potential - the same level as it would be if no charges were present at all!).

If electric field strength is zero it doesn't mean electric potential is also zero

A multiple choice question caused a lot of anxiety a couple of years ago.

It was a true/false type and this is statement that many thought was true:

"Electric potential is zero whenever the electric field strength is zero"

This is a FALSE statement, but many students couldn't see it was false !

Electric field strength or intensity is a vector - so if equal pulls or pushes act on the 'test particle' at the point in space you are looking at they will cancel each other out.

BUT the potential at that point in space will be subject to the change in potential due to the influence of all charges in the locality.

Look at the diagram. X is the mid-point between two identical positive charges::

The positive charges both push a positive test charge with equal force cancelling out the acceleration effect. The electric field strength at that point is therefore zero.

BUT both charges have an effect on the electric potential of point X.

The presence of one of them makes it harder to bring unit positive charge from infinity but the presence of the second one makes it twice as hard!.

It is as if that point in 'electric space' is raised twice as high by the second charges presence.

You can think of electric potential as "pressure."

Consider the following analogy: if two people push on a balloon with equal force, one on each side, the sum force will be zero - no net force, but the pressure in the balloon is higher than with true zero force being applied.