Topic Menu

Cyber-chess a chess instruction site

EMF and internal resistance

The Electromotive Force or EMF is the total energy transferred into electrical energy per unit charge by a voltage generator such as a battery or electrical generator.

It is given the symbolε - this is the Greek letter 'epsilon'

So, by definition:

ε = W/Q

where

W = total energy transferred

Q = unit charge

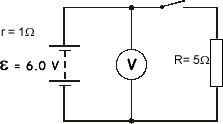
It is basically the potential difference across a cell, or other power suppl,y when the power source does not have to drive a current through an external circuit.

You can measure the EMF of a power supply by connecting a voltmeter in parallel with the supply alone, by opening the switch to the external circuit. This is called measuring the voltage 'on open circuit'.

Internal resistance and 'lost volts'

If you made up a simple circuit with a 6V battery to power it and connected a voltmeter across the battery you would find that the reading on the voltmeter would be 6V when the switch to the external circuit was open, but less than 6V when you closed the switch.

This is due to internal resistance in the cells of the battery.

Internal resistance

As the flow of electrons pass through the cell, energy is transferred from chemical energy stored in the cell to electrical energy as the electrons move. This process results in resistance within the battery itself and is known as the internal resistance of the battery. A particular battery will have a particular internal resistance.

What internal resistance means for voltage sharing

You know that voltage is divided 'fairly' between resistances. The bigger the resistance, the bigger the share of the voltage it gets.

Suppose we have a circuit with an external resistance of 5 ohms and an internal resistance of 1 ohm. 6V would share out so that the external resistance got 5V of it and 1V would be across the internal resistance.

Lost Volts

The potential difference measured on the voltmeter when the current flows though the circuit would be equal to the EMF of the battery (6V) minus the volts 'lost' due to the voltage drop across the internal resistance, r. It would therefore be 5V when the switch was closed. The voltage drop when closing the switch would be 1V - this is referred to as the 'lost volts'.

You know the equation for potential difference V = IR (Ohm's Law)

We now have a situation where the full voltage of the power supply - the EMF - is driving a current I through both an external resistance R and an internal resistance r. We therefore have:

ε = I (R + r)

(Ohm's law applied to the full circuit)

Note that the case of letters matters a lot when using an equation like this!

As ε = I (R + r) and I R = V (for the external circuit)

therefore we can substitute into the equation and get:

ε = V + I r

EMF = External circuit voltage + voltage driving current through the battery (lost volts)

lost volts ( ε - V) = I r

So if we know the current flow and the amount of the voltage drop on closing the switch, it is simple to work out the internal resistance of the cell.