Topic Menu

Cyber-chess a chess instruction site

Pressure in fluids

A fluid is something that can 'flow' - it has no fixed form.

A fluid can be either a liquid or a gas.

The pressure in a fluid causes a force normal (at right angles) to any surface it is in contact with - from the constantly moving particles pushing against the container walls. All force vectors for the impact with the sides can be resolved into horizontal and vertical components. The components that are perpendicular to the sides of the container create the pressure on the container - the ones parallel to it create no pressure.

So pressure is produced by a force at right angles to the surface and therefore by Newton's Third Law we know that the pressure from a gas produces a net force at right angles to any surface.

The pressure at the surface of a fluid can be calculated using the equation:

pressure = force normal to a surface/area of that surface

p = F/A

Where:

p = pressure, in pascals, Pa

F = force, in newtons, N

A = area, in metres squared, m2

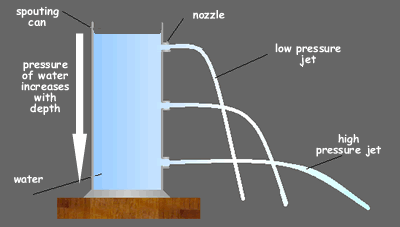
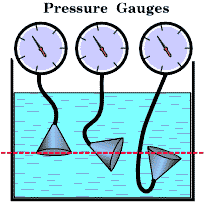
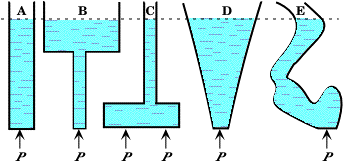
Pressure on an object within a fluid.

Within the fluid there is pressure.

If you immerse an object in a fluid it will feel the pressure of the atmosphere pushing down on the surface on the liquid and the additional weight of the column of liquid above it.

Let us consider how we can work this pressure out.

Pressure = force/contact area

If we consider an object immersed in a liquid it is being pushed down by a column of fluid above it. The contact area is the cross sectional area of that column of fluid above the object.

density of the liquid = mass/volume

ρ = m/V 

so,

mass = density x volume of the column

m = ρV

Now, the volume of the column is the height of column (h) x csa of column (A)

So.

mass of column = (density of fluid x height of column x csa of column)

m = ρhA

Now,

the force exerted by the weight of liquid in a column (F) = its mass x gravitational field strength (g)

F = mg

So,

the force = (density x height of column x csa of column) x gravitational field strength

F = ρhAg

and as pressure = force/area

the pressure exerted by the column of liquid = (density x height of column x csa of column x gravitational field strength )/csa of column.

p = F/A = ρhAg/A

So,

pressure = height of the column × density of the liquid × gravitational field strength

p = hρg

 

Hydrostatic Pressure in a Liquid

The spouting can shows that pressure increases with depth.

It consists of a tube with three separate nozzles in its side and an open surface on top. The three nozzles are blocked, then the tube is filled with water. When it is completely full, the holes are unblocked. The water is under more pressure the further down the tube it is. This is shown by the fact that the water jets travel a larger distance the lower the nozzle.

The pressure at a given depth within a liquid is due to the weight of the liquid acting on a unit area at that depth plus any pressure acting on the surface of the liquid (atmospheric pressure).

The pressure due to the liquid alone at a particular depth depends only upon the density of the liquid ρ and the distance that point is below the surface of the liquid - h.

It is therefore proportional to the depth.

 

 

 

The pressure at a given depth is independent of direction -- it is the same in all directions.

In this diagram we see the guages read the same because the pressure is being measured at the same depth (red line).

The pressure at a given depth does not depend upon the shape of the vessel containing the liquid or the amount of liquid in the vessel.

It only depends on the depth. In the diagram on the left, the pressure P is the same even though the containers have different amounts of liquid in them, and are different shapes.

Pascal's Vases:

The height of the liquid in each of the 'arms' of the vase is the same - even though they hold different volumes of liquid.