About this site
 |
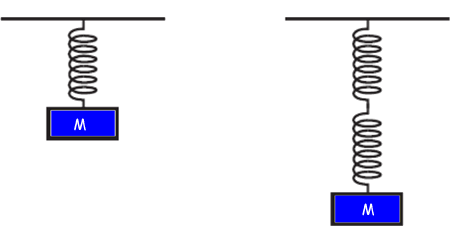
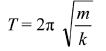Springs in series and parallel Up to A level you only have to consider sets of identical springs making up series and parallel combinations. Springs in series Each spring experiences the same pull from the weight of the mass it supports. Therefore each spring extends the same amount as an individual spring would do. The combination therefore is more 'stretchy' and the effective spring constant for the combination will be half that of a single spring for two in series, a third for three in series etc.
Springs in parallel The weight is supported by the combination. They share the load and therefore are not stretched as much as they would be if they were on their own supporting the load! The combination therefore is less 'stretchy' and the effective spring constant for the combination will be twice that of a single spring for two in parallel, a three times for three in parallel etc.
Combinations of springs exhibiting SHM When looking at 'bouncing masses' on spring combinations you need to remember that the spring constant has changed and this will affect the period of the oscillation.
Let's cancel out the constants and see how two changable variables relate. We can express T and k in terms of constants (m is kept the same so it is a constant) and that gives us: T√k= a constant We can therefore write: T1√k 1= T2√k 2 T2 = T1√(k 1/k 2)
|
Follow me...
|
Cyberphysics - a web-based teaching aid - for students of physics, their teachers and parents....
