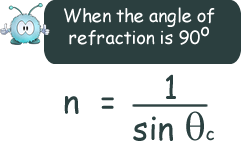Snell's Law - the refractive index
Snell's Law states that the ratio of the angle of incidence to the angle of refraction of a wave as it travels through a boundary between two media is a constant termed the refractive index - n - (which is the ratio of the indices of refraction). This is equivalent to the ratio of phase velocities in the two media (expressed as v or c), or equivalent to the reciprocal of the ratio of the indices of refraction. The value of this constant 'n' is equal to the ratio of the 'wavespeed' before and after it crosses the boundary.
1n2 is the inverse of 2n1...... to swap them round you simply find the reciprocal (see interactive spreadsheet) I talk in terms of OPTICAL media on this page - but there is nothing to stop the examiners talking about sound - remember is is the SPEED CHANGE that makes refraction occur - look carefully at the basic refraction page and follow the link to geophysics and refraction of sound.
If you carry out an experiment and measure the angle of incidence and the angle of refraction you will find that if you plot the sine of the angle of incidence against the sine of the angle of refraction you get a straight line that goes through the origin.
This indicates that the sine of the angle of incidence is directly proportional to the sine of the angle of refraction and that the ratio of the two will produce a constant value that we call the refractive index. The ratio of the sines of the angles is equal to the ration of the speeds of the waves through the media.
Always sort out in your mind what is happening to the speed of the wave as it crosses into the new medium before you start the maths. Critical AngleIf the angle of refraction is 90o then the angle of incidence is called the critical angle and is given the symbol 'c'. The sine of 90o is 1 so the equation becomes: sine of the critical angle = the refractive index This is going from an optically dense to an optically rare medium so the result will be <1
In this equation 'n' is quoted for rays going from the rare optical medium to the denser one (slowing down!)
LOJ April 2003 revised March 2021 |
Follow me...
|


 Snell's Law gives a mathematical
relationship to the observations of refraction made at GCSE.
Snell's Law gives a mathematical
relationship to the observations of refraction made at GCSE.
 Remember
Remember