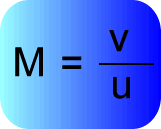Topic Menu

Cyber-chess a chess instruction site

The Lens Equation

In optics we work out the position, nature and size of the image produced by a lens.

We can do this either by accurate drawing of optical diagrams or by using the lens equation. In examinations you are often given the chance to choose which you would like to use.

Click here to go to the page on how to construct diagrams of how rays pass through lenses

Lens diagrams give a visual representation of the image formation but the lens formula makes up for any imperfections in your drawing skills!

It gives an accurate calculation of the position of the image - the sign giving you an indication of whether it is real or virtual. A positive sign indicates a real image (formed on the opposite side of the lens from the object) and vice versa. 

 

 

A length measurement should strictly be done in metres. If it is not you will have to think carefully about the units of any related physical quantity found from a formula using that length.

It does not matter if you work in 'cm' or 'mm' with this equation, as long as you are consistent. 

However if you are going to find the power of the lens in dioptres you must work out the focal length in metres first.

 

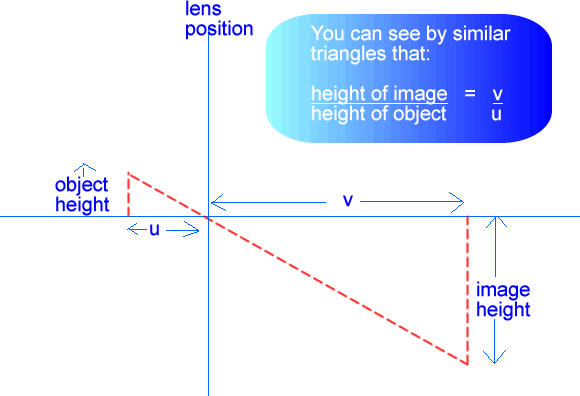
A convex lens has a real focus - therefore the power of a convex lens is a positive value. If you are longsighted the optomotrist will prescribe you a lens with a positive power value.

A concave lens has a virtual focus - therefore the power of a concave lens is a negative value. If you are shortsighted the optomotrist will prescribe you a lens with a negative power value.----------------------------------------

The magnification of a lens is the ratio of the size of the image to the size of the object (how many times bigger the image is than the object was!). If the ratio is greater than one the image is bigger than the object (enlarged) and if it is less than one it is smaller than the object (diminished in size). We can relate object and image size to similar triangles:

 

 

We therefore get a simple equation to work with:

 

 

Since v is in metres, and u is in metres, M has no units.

Return to the Lens Page