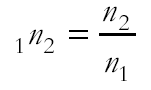Topic Menu

Cyber-chess a chess instruction site
Snell's Law

Consider the ray going through this composite block.

  • Angle of refraction at boundary AB (beta) is the angle of incidence at boundary BC (corresponding angles)
  • (Same for the 'gammas' in the next medium)
  • The ray is speeded up by the same amount it is slowed down (it has to be travelling at its original speed by the time it gets iback into the original medium!). Therefore the 'alpha' angles are the same.

Now by Snell's Law n = sin i / sin r, so

AnB = sin a /sin b

and

BnC = sin b / sin g

and

CnA = sin g / sin a

So we can 'jiggle' these equations around to get the refraction at the interior boundary in terms of the refractive indices of the two exterior ones...

BnC = sin b / sin g = (sin a /AnB ) / (sin a / CnA) = CnA/AnB

 

So..... BnC= CnA/AnB

This is given on your data sheet as