Topic Menu

Cyber-chess a chess instruction site

The Pendulum - energy transitions

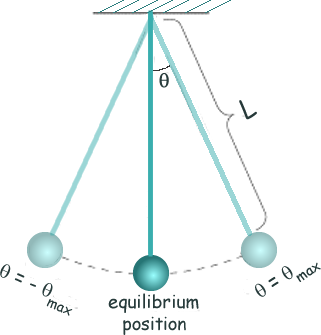
Consider a point pendulum bob connected to a massless rope or rod that is held at an angle q from the horizontal. If you release the mass, then the system will swing to a position at an angle q from the horizontal on the other side and back again to its starting position. This is one full period of the swing.

It can be determined that:

where

T is the period, or time for one complete swing,

l is the length - the distance from the point of suspension to the center of gravity of the bob. Care has to be taken that the point of suspension is a point - this can be achieved by clamping the string frimly between two pieces of card.

g is the acceleration of gravity.

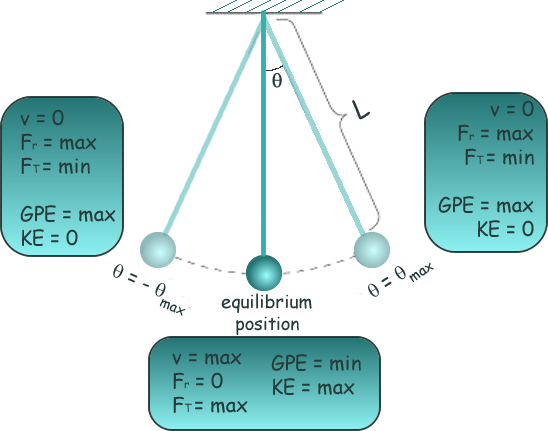
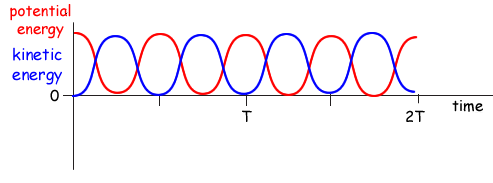
Energy Transitions

The mechanical energy of the ideal pendulum is a conserved.

The gravitational potential energy of the pendulum, mgΔh, increases with the height of the bob, therefore the potential energy is minimized at the equilibrium point and is maximized at the extreme positions.

Conversely, the kinetic energy and velocity of the pendulum are maximized at the equilibrium point and minimized at the extremes..