Topic Menu

Cyber-chess a chess instruction site

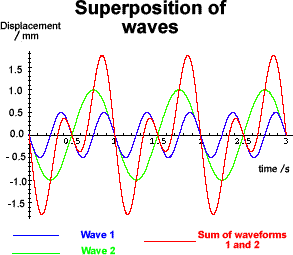
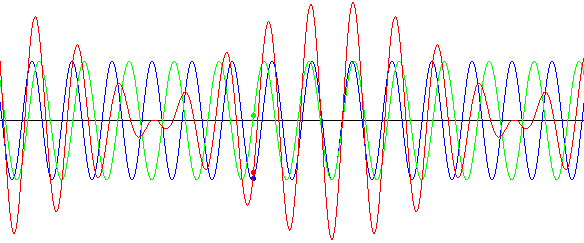
Superposition of Waves

Superposition of waves is simply finding the net effect that more than one waveform has on a medium.

A wave's displacement is either positive or negative at a point in time and space. If more than one wave is at that point in time and space then a 'net effect' will be observed.

If two waves travel towards each other the waves will 'add together' the amplitudes of vibration of the individual waves - they will interfere with one another:

Consider two waves of the same frequency and amplitude travelling towards each other (in opposite directions).

When they interact if he waves are in antiphase at that moment in time they will cancel each other out.

Two waves that are in phase (temporally) will result in a net wave envelope of the same frequency, and two waves that are in phase (spatially) will result in a wave envelope of the same wavelength. However the waves will  have double amplitude! (See coherence)

When waves are slightly out of phase the wave envelope is very interesting.

Consider the blue and green waveforms below. They are slightly out of phase.
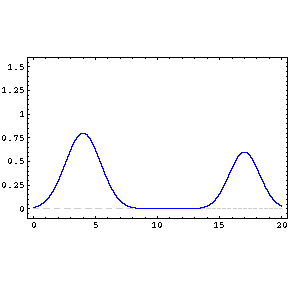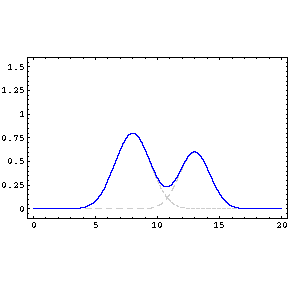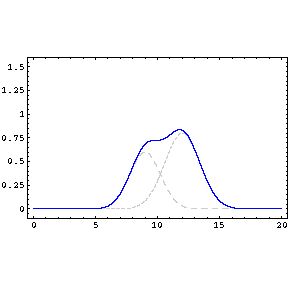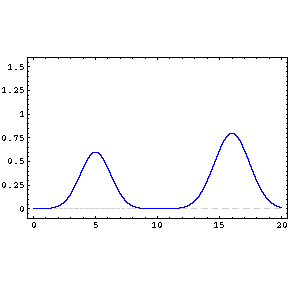
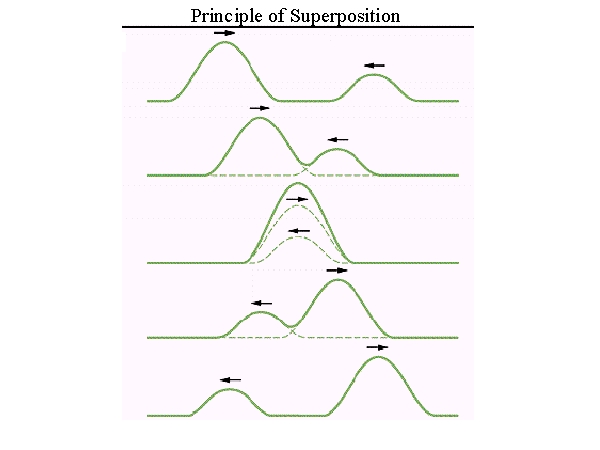
The red waveform is the 'net result' of the two waveforms travelling through a medium.

The summing of the waves gives rise to 'beats' - variations in amplitude that occur at a regular interval. The more in phase the green and blue waves are the longer the beat period would be. This is used to tune instruments such as the guitar.

The principle of superposition may be applied to waves whenever two (or more) waves are travelling through the same medium at the same time.

The waves pass through each other without being disturbed (see animated image below)

The net displacement of the medium at any point in space or time (the blue line), is simply the sum of the individual wave dispacements. The doted lines are included so that you can observe that the two waves do indeed 'pass' each other undisturbed.

This applies to both for waves which are finite in length (wave pulses) or which are continuous sine waves.
 
 
See standing waves

Here is a link to a program that gives you practice at understanding the equation of a wave (mathematically)