| 3.7.2.1 Newton's law |
Gravity as a universal attractive force acting between all matter.
Force between point masses
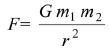
where G is the gravitational constant. |
Remember that gravitational force is one of the four fundamental forces.
It is only an attractive force.
Acts between masses.
Is an inverse square relationship
MS 0.4 Students can estimate the gravitational force between a variety of objects. |
| 3.7.2.2 Gravitational field strength |
Concept of a gravitational force field as a region in which a body experiences a gravitational force.
Representation of a gravitational field by gravitational field lines.
g as 'force per unit mass' defined by:
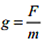
Magnitude of g in a radial field given by:
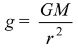
|
|
| 3.7.2.3 Gravitational potential |
Understanding of the definition of gravitational potential, including zero value at infinity.
Understanding gravitational potential difference.
Work done in moving mass m given by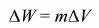
Equipotential surfaces.
Idea that no work is done when moving along an equipotential surface.
Magnitude of V in a radial field given by: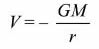
Significance of the negative sign.
Graphical representations of variations of g and V with r.
V related to g by: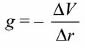
∆ V from area under graph of g against r.
|
Gravitational potential is energy...
Remember that measurements are from the centres of mass - strictly speaking the masses should be point masses.
MS 3.8, 3.9 Students use graphical representations to investigate relationships between V, r and g.
|
| 3.7.2.4 Orbits of planets and satellites |
Orbital period and speed related to radius of circular orbit.
Derivation of T2 ∝ r3
Energy considerations for an orbiting satellite.
Total energy of an orbiting satellite.
Escape velocity.
Significance of a geosynchronous orbit.
Use of satellites in low orbits and geostationary orbits, to include plane and radius of geostationary orbit. |
You do not need all of Kepler's Laws - but they are good for your soul...
MS 0.4 Estimate various parameters of planetary orbits, eg kinetic energy of a planet in orbit.
MS 3.11 Use logarithmic plots to show relationships between T and r for given data. |


