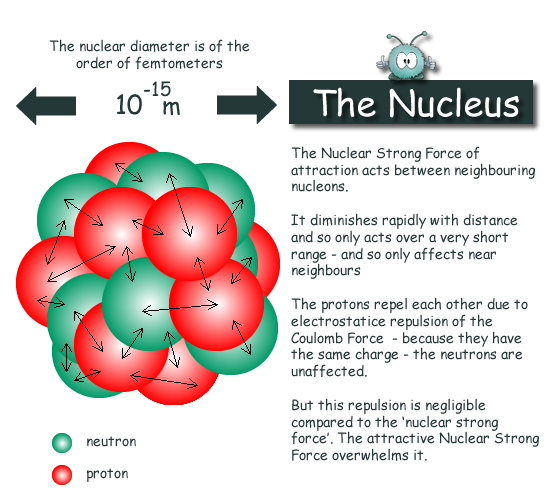
The Atomic Nucleus

 

The nucleus of an atom contains nucleons: protons and neutrons.

Protons repel each other via the Coulomb force but over a very short range (femtometres) there exists a very strong force called the strong nuclear force. This binds the nucleons together into a nucleus.

Nuclei are typically femtometres in diameter - (a femtometre (fm) is 10^-15m).

To view a scaled diagram of an atom on your computer screen with a nucleus of 1 cm diameter in the centre you would need a screen of 1km diameter to show the full graphic!

The nucleus is tiny compared to a whole atom.

It occupies one part in 100,000,000,000,000 of the atomic volume

The number of protons (Z) determines the chemical properties of the atom - which element it belongs to - it is called the proton number or atomic number.

The number of neutrons (N) affects its physical properties - which isotope of the element it belongs to.

The mass number (A) or nucleon number is the number of protons plus the number of neutrons

The specific charge of a nucleus is the total charge of the nucleons (in coulombs) divided by the total mass of the nucleons (in kilograms).

Specific charge is measured in C^-1kg

Various types of scattering experiments suggest that nuclei are roughly spherical and appear to have essentially the same average density.

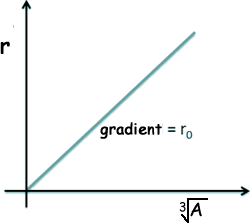
This is studied at A level and is deduced from the following equation - where r is the radius of the nucleus of mass number A.:

This equation can be deduced from the following reasoning:

The mass of the nucleus will depend on A - the number of nucleons in the nucleus - as they have virtually the same mass :

Nuclear mass = Am

where

A = nucleon number and

m = the mass of a nucleon

Assuming the nucleus is spherical we have a volume:

V = ⁴/₃πr³

Density = mass / volume

So,

ρ = Am/(⁴/₃πr³)

ρ = 3Am/(4πr³)

m and  are constant - there is therefore a constant value of 3m/(4π) and we can say that:

Density is proprtional to A/r³

 

Rearranging this we get that r is proportional to the density divided by the cube root of A

If we call the constant of proportionality r_o we get the above equation.

If r is plotted against A^1/3 a straight line is obtained - the gradient of it is the constant r_o - but the relationship is best for large values of A so if you use small values this does not work too well!

To show that nuclear density is independent of A in other words that all nuclei have the same density - or uniform density

Let the  volume of a nucleus be V

the mass of the nucleus be M

and the mass of a nucleon be m

V = ⁴/₃r³

ρ = M/V

So, M = ⁴/₃πr³ρ

Let's replace the r³ in this expression by using the equation above for r

so, r³ = r_o³A

M = ⁴/₃πr_o³A ρ

but M = Am

So, Am = ⁴/₃πr_o³A ρ

Therefore,

Rearranging we get, ρ = 3m/(4πr_o³ )

This means that the density does not depend on A or on r - it is related to constant values - it is therefore a constant value and uniform.

Data relating to nuclear size

The most definitive information about nuclear sizes comes from electron scattering experiments.

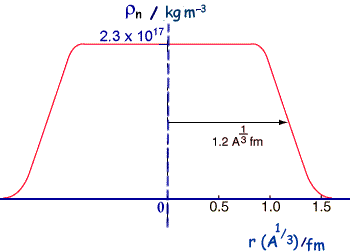
If we compare calculated and experimental radii for nuclei we find that that there is an area around the edge of the nucleus where the density of nuclear matter decreases toward zero - but that the central part is roughly of constant density. So the nucleus cannot be thought of as just a hard sphere.

The fact that the nuclear density is independent of the details of neutron number or proton number suggests that the force between the particles is essentially the same whether they are protons or neutrons.

This agrees with other evidence that the strong force is the same between any pair of nucleons.

Techniques employed to study the nucleus

Electron Diffraction

Alpha Particle scattering

Ready for some questions? Click on the icon - questions and answers at A level standard await you! For more topics that have practice questions associated with them see the top menu bar - examination preparation