Capacitor Discharge

Graphical Representation and Quantitative Treatment of Capacitor Discharge

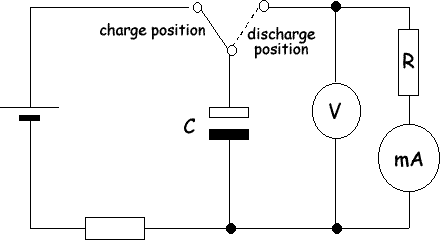
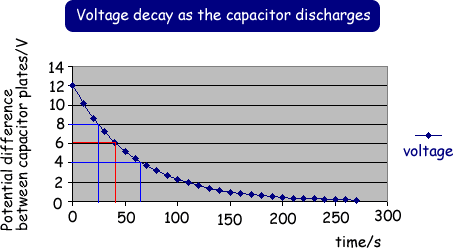
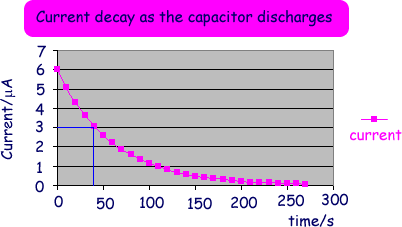
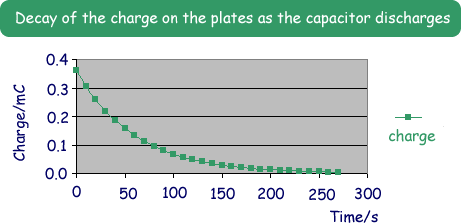
The decay of charge in a capacitor is similar to the decay of a radioactive nuclide. It is exponential decay. If we discharge a capacitor, we find that the charge decreases by half every fixed time interval - just like the radionuclides activity halves every half life.  If it takes time t for the charge to decay to 50 % of its original level, we find that the charge after another t seconds is 25 % of the original (50 % of 50 %).  This time interval is called the half-life of the decay.  The decay curve against time is called an exponential decay.

 

The voltage, current, and charge all decay exponentially during the capacitor discharge.

We can perform an experiemnt to obtain the data for us to plot a graph to show this by using the circuit below:

 

We can charge up the capacitor and then flip the switch and record the voltage and current readings at regular time intervals and plot the data, which gives us the exponential graphs below. 

Let us use a voltage of 12V to charge up a 30F capacitor and have resistance R as 2 M

Note the following about the graphs:

• The half life of the decay is independent of the starting voltage.

• The current  follows exactly the same pattern (as I = V/R)

.

Note that the 'half life' is the same as for voltage

• The charge follows the same pattern, as Q = CV.

The graphs are asymptotic (like the one for radioactive decay) , i.e. in theory the capacitor does not completely discharge but in practice, it does.

 

The graph is described by the relationship:

 

Q = Q₀ e ^–t/RC

Compare this to the radioactive decay equation:

the decay constant is equivalent to ¹/_RC

The product RC (capacitance of the capacitor × resistance it is discharging through) in the formula is called the time constant.  The units for the time constant are seconds.

 

We can show that ohms × farads are seconds.

unit of R = ohms; unit of capacitance = farads

but V=IR so unit of resistance is V/A and C = Q/V so th unit is C/V

unit of product is therefore C/A... but an amp is a coulomb per second so the unit is the second!

  So if we discharge the capacitor for RC seconds, we can easily find out the fraction of charge left:

           

            V= V₀ e ^–RC/RC = V₀ e ^–1 = 0.37 V₀

 

So, after RC seconds the voltage is 37 % of the original. 

 

This fact is used widely by electronic engineers.  To increase the time taken for a discharge we can:

• Increase the resistance.

• Increase the capacitance.

We can link the half-life to the capacitance. 

At the half life:

Q = ¹/₂ Q₀

t = t_1/2

Q₀/2 = Q₀ e ^{– t}_1/2^/RC

 

½ = e ^{– t}_1/2^/RC

 

2^-1 = e ^{– t}_1/2^/RC

 

e ^{+ t}_1/2^/RC = 2

 

ln (2) = t_1/2/RC 

 

t_1/2  = log_e (2) × RC

 

t_1/2 = 0.693 × RC

 

So, the half-life is 69.3 % of the time constant.

 

Capacitors - an introduction Capacitance - definition and equations Dielectric The parallel plate capacitor Storing Energy in a Capacitor An Experiment to Determine the Capacitance of a Capacitor

Ready for some questions? Click on the graphic - Multiple Choice questions and answers at A level standard await you! For more topics that have practice questions associated with them see the upper left menu bar

 

Ready for some questions? Click on the graphic - Short Response questions and answers at A level standard await you! For more topics that have practice questions associated with them see the upper left menu bar