Storing Energy in a Capacitor
Stored energy
As opposite charges accumulate on the plates of a capacitor due to the separation of charge, a voltage develops across the capacitor due to the electric field of these charges. Ever-increasing effort must be put in against this ever-increasing electric field as more charge is separated - work has to be done.
The energy (measured in joules) stored in a capacitor is equal to the amount of work required to establish the voltage across the capacitor, and therefore the electric field.
We know that W=QV (energy or work done = charge x potenetial difference)
and Q = CV
Let us plot a graph of charge against potential difference
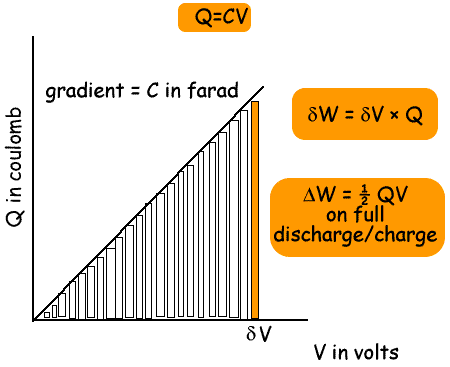
The capacitor is charged with charge Q to a voltage V.
If we discharged the capacitor by a tiny amount so the potential difference drops,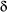 
V. The resulting tiny energy loss (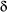W) can be worked out from the first equation:
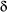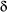W = V × Q
This is the area of the orange rectangle on the graph.
If we discharge the capacitor completely, we can see that:
Energy loss = area of all the little rectangles
= area of triangle below the graph
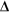W (for a capacitor charge or dischage) = ½ QV
OR
Let us plot a graph of potential difference against charge:
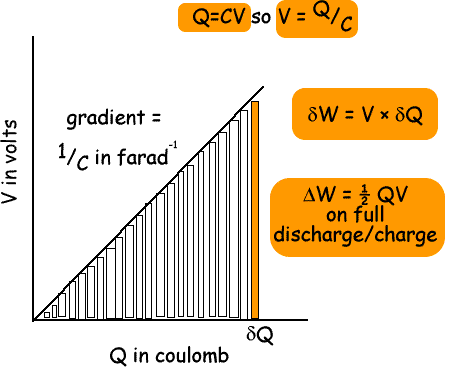
The capacitor is charged with charge Q to a voltage V.
If we discharged the capacitor by a tiny amount of charge, 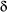Q. The resulting tiny energy loss (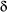W) can be worked out from the first equation:
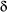W = V × 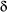Q
This is the area of the orange rectangle on the graph.
If we discharge the capacitor completely, we can see that:
Energy loss = area of all the little rectangles
= area of triangle below the graph
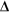W (for a capacitor charge or dischage) = ½ QV
Both methods give us the same outcome!
Now, as Q=CV
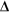W (for a capacitor charge or dischage) = ½ CV2
or 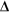W (for a capacitor charge or dischage) = ½ Q2/C
On your data sheet you are told that the energy stored is given by:
-
where V is the voltage across the capacitor - Q is the charge deposited on each plate - you are expected to remember that Q=CV and to work out the other versions of this equation!.
The maximum energy that can be (safely) stored in a capacitor is limited by the maximum electric field that the dielectric can withstand before it breaks down. Therefore, capacitors of the same type have about the same maximum energy density (joules of energy per cubic metre).
 |
Ready for some questions?
Click on the graphic - Multiple Choice questions and answers at A level standard await you!
For more topics that have practice questions associated with them see the upper left menu bar
|
|
Ready for some questions?
Click on the graphic - Short Response questions and answers at A level standard await you!
For more topics that have practice questions associated with them see the upper left menu bar
|
About this site
