The Young Modulus (E)- the modulus of elasticity

The Young Modulus is named after Thomas Young (1773 to 1829) who was a British polymath, contributing to our understanding of optics, physiology, and Egyptology, among other fields

The Young Modulus is also known as Young's Modulus or the elastic modulus or tensile modulus.

It is a measure of the stiffness of a material that is independent of the particular sample of a substance. That means a generic value can be given for a material without its dimensions being known (like the values given for resistivity).

It is the ratio of tensile stress (force/cross sectional area) to tensile strain (extension/ original length) - don't forget to put the word 'tensile' into any definition you give in an exam - it will lose you marks!

 

 

The unit will therefore be the same as the unit of pressure (Pa or N/m²)

 

Quantity	Equation	Symbol	Units
Stress	tension/cross sectional area = F/A	(sigma) σ	N m-2 = Pa
Strain	extension per original length = ΔL/L	(epsilon) ε	no units (because it’s a ratio of two lengths)
Young Modulus	stress/strain	E	N m-2 = Pa

 

Strain values can be expressed in several ways: as a percentage - %, or in decimal form. E.g. a 5% strain = 0.05

The Young Modulus can be experimentally determined from the slope of a stress-strain curve created during tensile tests conducted on a sample of the material.

The value of the Young's Modulus is quoted in scientific data manuals for various materials but the value given is only approximate. This is because Young's Modulus can vary considerably depending on the exact composition of the material. For example, the value for most metals can vary by 5% or more, depending on the precise composition of the alloy and any heat treatment applied during manufacture.

If a big force only produces a small extension then the material is 'stiff' and E is a big value.

If a force produces a big extension then the material is not very stiff - it is easier to stretch and the value of E will be smaller.

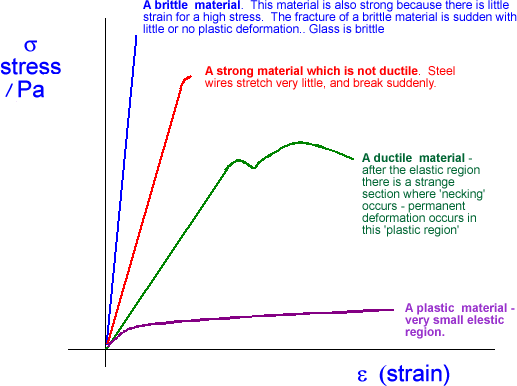
Linear vs non-linear behaviour

For many materials, Young's modulus is a constant over a range of strains. Such materials are called linear, and are said to obey Hooke's law. Examples of linear materials include steel, carbon fiber, and glass. Rubber and soil (except at very low strains) are non-linear materials.

 

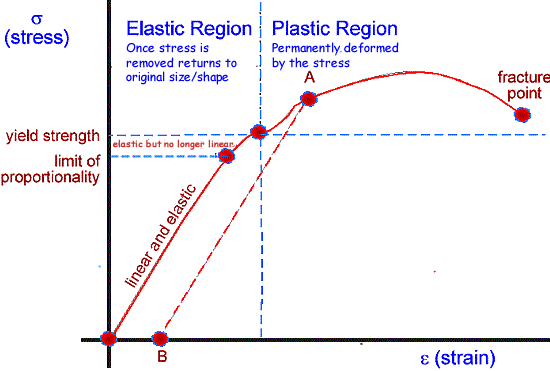
This stretching behavior is summarized in a stress-strain graph such as the one above.

As the stress is increased initially Hooke's Law is obeyed - the stress-strain relationship for the wire is linear and elastic.

Just before the plastic region is reached we get the limit of proportionality - beyond this for a small section we see non-linear behaviour but the stretching is still elastic.

After the yield strength, the material enters the plastic deformation region, which means that the stretch of the wire is permanent. (For example, if the wire is stressed to point A on the graph and the stress is slowly decreased, the stress-strain curve follows the dotted line instead of the original curve to point B and there is a permanent extention when all stress is removed.) At the facture point the wire reaches its snaps.

Differences in the shape and limits of the stress-strain diagram determines whether a material is considered ductile or brittle, elastic or plastic.

Click here to find out about the Young Modulus

Click here to see notes on an experiment to determine the Young Modulus.