Topic Menu

Cyber-chess a chess instruction site

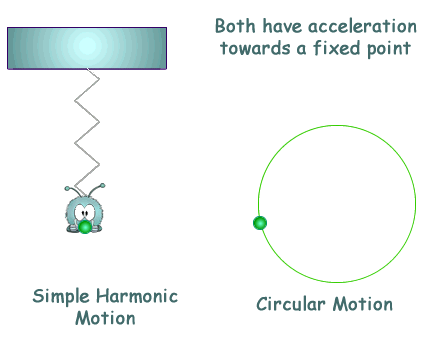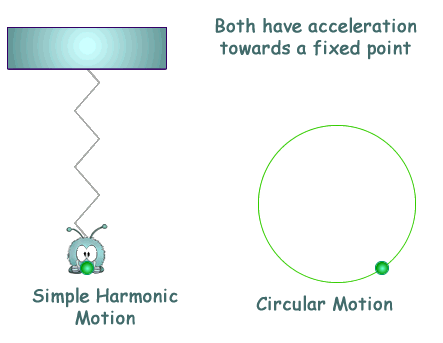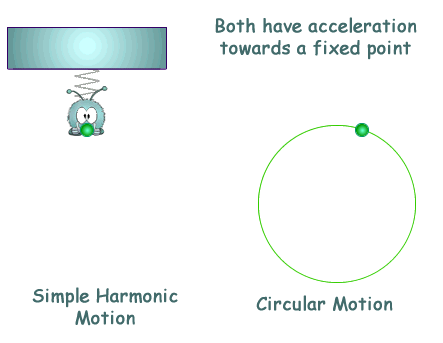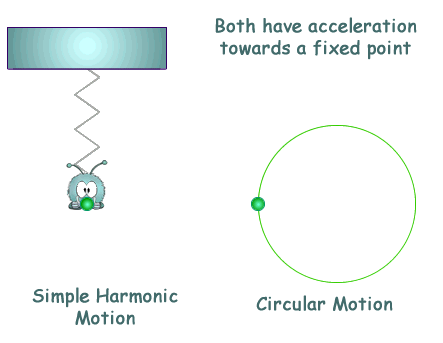
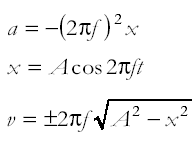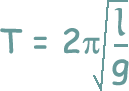Simple Harmonic Motion

Simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. It results in an oscillation which, if uninhibited by friction or any other dissipation of energy, continues indefinitely.

Wow! What a mouthful!...

SHM is an important topic because it describes mathematically the natural vibrations we see everywhere around us. If you 'disturb' a branch on a tree or a spider suspended on his web, the 'rocking motion' you observe is SHM - the system exhibits shm as the natural foces ply to restore the equilibrium you disturbed with your 'driving force'.

Lots of natural systems exhibit SHM - bouncing, swinging, vibrating things are all usually moving in SHM: from atomic vibrations to suspension bridges!

It is therefore an important topic for engineers.

The characteristic features of simple harmonic motion

    Acceleration is proportional to the distance from a fixed point in its path

    Acceleration is directed TOWARDS that point.

This is like circular motion where the acceleration is towards the centre of the circular path. See this page for more on the similarity between SHM and circular motion.

Graphical and analytical treatments

Understanding and use of the following equations:

The characteristic features of simple harmonic motion are summed up in the first equation (NB you must always mention both characteristics!)

Acceleration (a) is proportional to the distance (x) from a fixed point in its path

Acceleration is directed TOWARDS that point (hence the negative sign in the equation below!)

a= -w2x

a = - (2pf)2x

 

The constant of proportionality is w2

A strange constant you may think! .... but, in order to understand where it comes from we have to do a bit of mathematical analysis.

w is the angular velocity of the circular motion that corresponds to the SHM.

It is equal to 2pf where f is the frequency of the sinusoidal waveform that is associated with SHM. (See how SHM relates to circular motion).

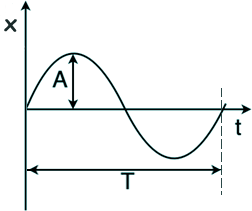
Now, at what point should we begin timing? Does it matter?

Well, no, not really, the motion is still SHM...

But the mathematical desription of the motion will alter depending on where we begin the cycle!

If we time from the centre of the oscillation (where x=zero at time t=0s) we get a sine curve to describe the displacement as time varies, if we time from a point where x=A (maximum displacement) we get a cosine curve, but either way, after a bit of mathematical analysis, we get rid of the original trig function for displacement and get 'a' in terms of 'x' and a constant!

Let me show you how:

Mathematical treatment 1 (t=0 when x=0)

In a graph of displacement against time for a particle exhibiting SHM the amplitude of the graph would be A and the equation would be:

x = A sin wt

The differential (gradient with respect to time) of this equation would give the velocity 'v'.

v = A w cos wt

The differential (gradient with respect to time) of this equation would give the acceleration 'a'.

a = -A w2 sin wt

BUT

A sin wt = x

so

a = -Aw2 sin wt = -w2x

Mathematical treatment 2 (t=0 when x=A)

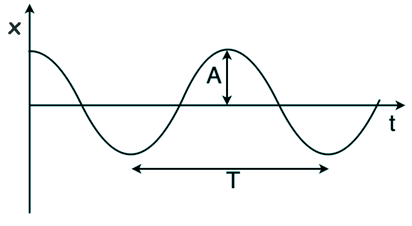
In a graph of displacement against time for a particle exhibiting SHM the amplitude of the graph would be A and the equation would be:

x = A cos wt

The differential (gradient with respect to time) of this equation would give the velocity 'v'.

v = -Aw sin wt

The differential (gradient with respect to time) of this equation would give the acceleration 'a'.

a = -Aw2 cos wt

BUT

A cos wt = x

so

a = -Aw2 cos wt = -w2x

BOTH treatments have the same result! Care when tackling questions that you choose the correct trig function - the one in your syllabus - to describe the situation given in the question - look to what is happening when t=0s!!

 

Note that the equation has acceleration 'a' proportional to the negative value of the displacement' x' (i.e. proportional to the distance (magnitude of the displacement!) but opposite in direction - acceleration increases as it gets closer to the point we are measuring from.

The constant of proportionality is linked to the frequency 'f' of the oscillation. Therefore the general equation for SHM could be written:

a = - (2pf)2x

Now

v = - Aw sin wt

So

v2 = A2w2 sin2wt

But

sin2wt + cos2wt = 1

so

v2 = A2w2 (1-cos2wt)

v2 = A2w2 - A2w2cos2wt

However we know that:

Acoswt = x

Squaring this we get:

A2cos2wt = x2

Therefore, by substituting it into our equation we get:

v2 = A2w2 - w2x2

And taking the square root of this we get:

v = +w(A2 - x2)0.5

or

You are GIVEN this on the data sheet - you do not have to worry about deriving it - this just shows where it comes from (same thing can be done with the sine expression... try it!)

This equation gives the velocity at any displacement x.

If it is at the extremities x=A therefore the velocity is zero.

At the centre of the oscillation x=0 so v= wA=2pfA (maximum velocity) the +/- indicates the direction of travel.

You should be able to sketch the graphs of displacement, velocity and acceleration against time for a system operating SHM.

If you start at the point x=0 at time t=0 then the displacement graph will be a sine curve (amplitude A), the velocity a cos curve (amplitude wA) and the acceleration a negative sine curve (amplitude w2A) - where w is 2pf.

If you start at a distance A from the point x=0 at time t=0 then the displacement graph will be a cosine curve (amplitude A), the velocity a negative sine curve (amplitude wA) and the acceleration a negative cosine curve (amplitude w2A) - where w is 2pf

Exchange of potential and kinetic energy in oscillatory motion

The energy of the system is taken to be constant - made up of kinetic (max at x, where velocity is a max and zero at A because velocity at A is zero) plus potential which has the opposite characteristics of the kinetic.

See this page.

Graphical representations linking displacement, velocity, acceleration, time and energy

You should know how to skech and interpret displacement/time and velocity time graphs for SHM.

You should know that velocity is the gradient of displacement/time graph and

Acceleration the gradient of a velocity time graph.

You should know that the amplitudes of the graphs are related by a factor of 2pf = w

Kinetic energy will follow the velocity squared graph - NEVER goes negative! (and Potential energy plus KE = constant!)

Simple pendulum and mass-spring as examples and use of the equations:

The pendulum as an example of SHM - 'g' is gravitational field strength and 'l' is the length. The period will vary according to which planet you are on.

The mass on a spring - 'm' is the mass (kg) and 'k' is the spring constant (stiffness of it (which relates to interatomic forces) - revise Hooke's Law!). This will not vary according to the planet it is on!

A light gate can be used to detect the times that a swinging pendulum or bobbing mass on a spring cast a shadow over it. This is a more accurate and less tedious way of finding the period (and hence the frequeny) of an oscillation. (The syllabus specifies that you should be aware of this!).