The Oscillation of a Spring

Consider a mass, m, placed on a frictionless surface (therefore there will be no energy transfer out of the system!), and attached to a wall by a spring.

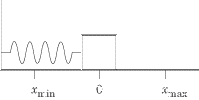
In its equilibrium position x = 0 the mass is at rest.

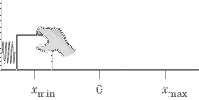
Let us push the mass toward the wall, compressing the spring, until the mass is in position x_min.

 

When you release the mass, the spring will exert a force, pushing the mass back until it reaches position x_max.
Now the spring will be stretched out, and will be exerting a force to pull the mass back in toward the wall. Because we are dealing with an idealized frictionless surface, the mass will not be slowed by the force of friction, and will oscillate back and forth repeatedly between x_max and x_min.

Hooke’s Law
The force, F, that the spring exerts on the mass is defined by Hooke’s Law:

F = -kx

where:

x is the spring’s displacement from its equilibrium position and

k is a constant of proportionality called the spring constant.

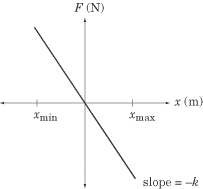
The spring constant is a measure of “springiness”: a greater value for k signifies a “tighter” spring, one that is more resistant to being stretched.

Hooke’s Law tells us that the further the spring is displaced from its equilibrium position (x) the greater the force the spring will exert in the direction of its equilibrium position (F). We call F a restoring force: it is always directed toward equilibrium.

Because F and x are directly proportional, a graph of F vs. x is a line with slope –k.

Simple Harmonic Oscillation

A mass oscillating on a spring is an example of a simple harmonic motion as it moves about a stable equilibrium point and experiences a restoring force proportional to the oscillator’s displacement.

For the oscillating spring, the restoring force, and therefore the acceleration (as F=ma), are greatest and positive at the extremes and zero at x = 0.

Important Properties of a Mass on a Spring

The period of oscillation, T, of a spring is the amount of time it takes for a spring to complete a full cycle. Mathematically, the period of oscillation of a simple harmonic oscillator described by Hooke’s Law is:

 

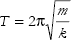
This equation tells us that as the mass of the block, m, increases and the spring constant, k, decreases, the period increases. In other words, a heavy mass attached to an easily stretched spring will oscillate back and forth very slowly, while a light mass attached to a resistant spring will oscillate back and forth very quickly.

The frequency of the spring’s motion tells us how quickly the object is oscillating, or how many cycles it completes in a given timeframe. Frequency is inversely proportional to period.

Frequency is given in units of cycles per second, or hertz (Hz).

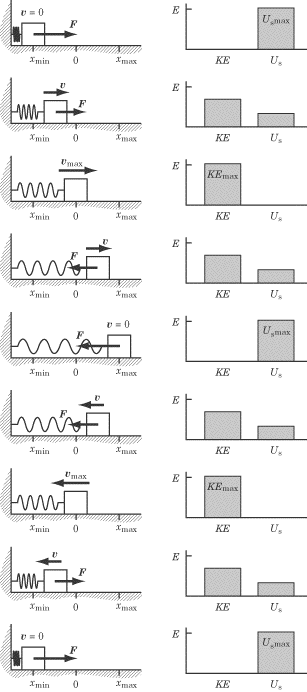
The potential energy of a spring is sometimes called elastic energy, because it results from the spring being stretched or compressed. Mathematically it can be found as the maximum kinetic energy of the spring's mass.

The potential energy of a spring is greatest when the coil is maximally compressed or stretched, and is zero at the equilibrium position. Hence the potential energy, is zero at the midpoint and the mechanical energy is only due to the kineticl energy.

At the points of maximum compression and extension, the velocity, and hence the kinetic energy, is zero and the mechanical energy is only due to the potential energy.

 

Vertical Oscillation of Springs

Now let usconsider a mass attached to a spring that is suspended from the ceiling. The oscillation of the spring when compressed or extended won’t be any different, but we now have to take gravity into account.

Equilibrium Position

Because the mass will exert a gravitational force to stretch the spring downward a bit, the equilibrium position will no longer be at x = 0, but at x = –h, where h is the vertical displacement of the spring due to the gravitational pull exerted on the mass.

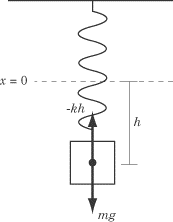The equilibrium position is the point where the net force acting on the mass is zero - the point where the upward restoring force of the spring is equal to the downward gravitational force of the mass.

The restoring force, F = –kh, and the gravitational force, F = mg, therefore

-kh = mg

and h=-mg/k

The mass displaces itself more if it has a large weight (mg) and is suspended from a spring with a small spring constant (slack spring!).

A Vertical Spring in Motion

If the spring is then stretched a distance d, where d < h, it will oscillate between (-h-d) and (-h+d).

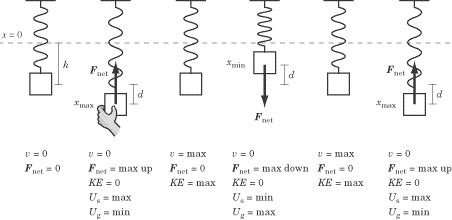
The force of gravity is constant and downward all of the time it is oscillating!

The restoring force of the spring is always upward, because even at x _(min) the mass is below the spring’s initial equilibrium position of x = 0.

Note that if d were greater than h the restoring force would act in the downward direction until the mass descended once more below x = 0.

According to Hooke’s Law, the restoring force decreases in magnitude as the spring is compressed. Consequently, the net force downward is greatest at x_min and the net force upward is greatest at x_max.

For springs in series and parallel click here

Graphics and notes adapted from sparknotes.com